We all have struggled with math in school because it looks quite confusing to a kid who has just started education. Math doesn’t look like a fair deal to the young learner, but worry not math can be fun too when learned through real-life examples. So let’s gear up to make this more fun and effective learning for your kid!
Ever went to the school fair on Children’s day and got 150 rupees to buy and eat whatever you want in the fair by your parents?. You can spend 1-150 rupees, and the minimum value is one rupee, and the maximum is one fifty rupees. Now this is your range of expenditure, and accordingly, you can make your purchases; you cannot exceed that maximum amount because that’s all you have. This is called the range and a similar concept is there in algebra. In this article, we will learn everything we should know about range in algebra; read till the end to see where you can head towards to learn more concepts and formulas in algebra.
What is Algebra?
Now to start with range, let’s touch the prerequisite but guess what it makes the concepts coming easier and also everyone needs revision when it comes to math, even us sometimes! So we will discuss a bit about the basics of algebra before talking about the more serious aspects of algebra.
Algebra is a mixture of constants, operators and variables fixed inside an equation and upon solving the equations we get the exact values of variables, and that’s fair because they had no names(values) before! So algebra is a lifesaver for variables, it helps them find their value, and that’s what a true friend does. So algebra solved the problem of variables and for the constants and operators played their part as well. Just imagine you have two friends; now you and one of your friends brought your lunch box for recess but one friend lost his tiffin box in the classroom itself. Now you both help that friend to find his lunch box so that you three can eat during the recess together. With your help, he finds the tiffin, and you three enjoy your lunch break together. Just imagine the one who lost his lunch box is variable and you two as constants and operators who helped to find the value of the variable i.e. lunch box. How you did it is algebra. Now that you have seen what algebra does and why you are ready to learn Algebra formulas and examples so that you grasp the concepts, let us go ahead with it.
Mathematical range
Range in algebra is also known as the co-domain of the algebraic functions.
To calculate the range of a given set of numbers, subtract the highest number with the lowest and the range of the series will be produced. But in algebra there exist mathematical functions that contain constants, variables, and operators, and to find the range of such equations let’s dive into functions because all the equations can be summarised into the umbrella term functions and from now on functions will be used to address the problems of equations and algebraic range.
Functions-An introduction
The dependence of one quantity over some set of variables and their interrelation inscribed in a mathematical equation is said to be a function. Everything around us can be described in the form of function. Let’s take the example of the area of a rectangle:
area=length*breadth(generic equation)
a= x*y (variable equation)
Now both the equations are nothing but functions as the variables have interdependence and operators and maybe constants. In case the length changes the area will change, and if breadth changes area will change or if the area has changed, then there must have been changing in breadth and length whatsoever. We deal with many such conditions day to day like the yield of a crop depends on the water supply and sunlight procured by the crops. The force depends on mass and acceleration. The thickness of wire and resistance are dependent on each other and endless examples. All these can be deduced in a functional equation and solved algebraically. The interesting part is the range of the algebraic functions obtained is the range of possible answers one could get upon solving the equation. The idea behind understanding functions is to get a clear idea about it’s resulting range.
Range calculation of a function
Let’s assume that we have functioned as f(x) and the resultant output as y, in this case, we have the following equations
y=f(x)
Now to find the range of this mathematical function would be like to see all the potential values of y that can exist. Upon calculating the range, there would be a set of values of y as the resulting range.
Take an example
y= √x-1 as the equation now upon inverting the function the range would be simply x=√y-1 and hence the range will be calculated like this.
To be precise, there are three steps to find the range of an algebraic function:
- Note the equation in the form y=f(x)
- Solve the equation and obtain an equation in terms of y from the same function
- If the equation isn’t solvable, then it would require a graphical approach.
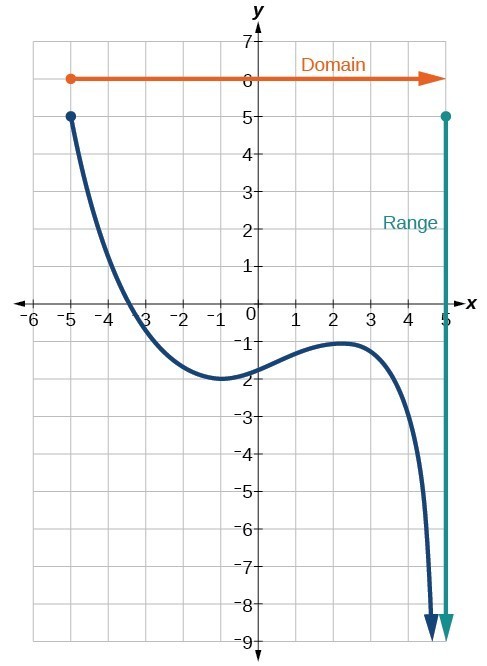
Ways to find the range of algebraic functions
It is the set of y-values that you get when you plug all of the possible x-values into the function. This set of possible x-values is called the domain. If you want to know how to find the range of a function, just follow these steps.
- Through given formula
Let’s say the formula is the following: f(x) = 4×2 + x -1. This implies that when you put the value of x, the value of y is obtained. This function is the equation of a parabola.
- Range of a function through relation
The relation is ordered pair collection, and just by looking at the relation set one can look for range and domain. For example the relation given is {(2,3),(-1,0),(4,6),(5,8). The y coordinates {3,0,6,8} are the range of the relation whose domain is the x coordinates{2,-1,4,5}. In a nutshell, the range for the given function is (0,8) if you look closely at the range set the lowest value the algebraic function had was 0, and the highest was 8.
- Through Graph
On higher levels, the range is calculated through graphs by either calculating the minimum and maximum points in through various point methods and is considered easier by mathematicians to read the graph and find values of range but that is covered in higher classes and has lots of technical calculations that require the prerequisite of calculus along with high-level computer software to sketch the accurate graph and their corresponding coordinates and hence the concept of finding range through graph has many layers and needs a thorough knowledge of graphs and calculus. The topic, however, is beyond the scope of this article and is kept intact for students of higher grades as it requires mathematical understanding to the extent that isn’t basic.
Conclusion
The range in algebra isn’t a cakewalk but also not rocket science. It is equally important in solving daily life problems related to mathematics and also helps in cross-checking the solved roots of any equation as the roots must lie in the range or else the calculated roots are wrong. The problem needs to be resolved and hence the range of any function holds practicality in real life as well. But generally, the maximum practice has required the range and domain calculation of functions because with an increase in grades the complexity of algebra increases there would be more types of number in existence including imaginary numbers and to hold them together and find out the resultant range inclusive of all becomes bit tricky but for easy understanding and grasp practice Algebra formulas and examples regularly because this will provide a variety of questions along with possible cases that can exist including exception based on algebraic range and hence more clarity about the concept will be gained. The topic has applications, in the long run, starting from the school books till graduation syllabus and not only in maths later on it will be an integral part of the physics curriculum, and hence individuals are expected to be clear with different methods and have ease with each of them.











