In differential calculus, the second-order derivative is used frequently to evaluate the second derivative of the same function. The differential is a branch of calculus used to measure the slope and the rate of change of given functions w.r.t its variables.
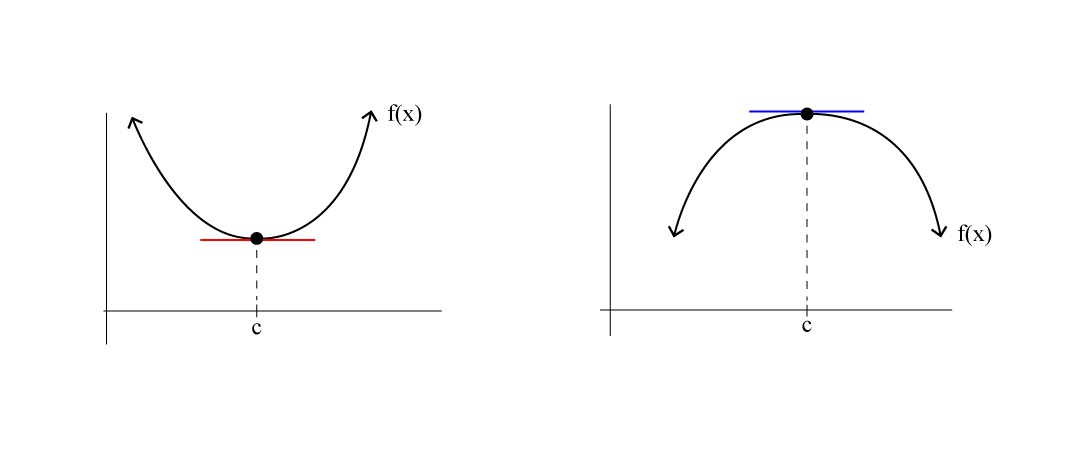
In this article, we will learn about the second derivative and how to find the second-order derivative of the functions with examples.
What is the second derivative?
The process of finding the derivative of a function w.r.t its variable is known as a derivative. Similarly, the process of finding the second-order differential of a similar function is known as a second derivative. It is often called a second-order derivative.
In simple words, a term is said to be a second-order derivative, if a function is differentiated two times with respect to its independent variable. You have to evaluate the differential of the function first, to differentiate the second-order derivative of a function.
The notation used for differentiation is d/dx. While the notation for second-order differential is
d2/dx2. Keep one thing in mind that you have to apply the second differentiation notation on the result of the first derivative, not on the given function.
Rules of the second derivative
The rules of differentiation are used in the second-order differentiation but have the notation of the second derivative.
| Names | Rules |
| Power rule | d2/dx2(xn) = d/dx[d/dx(xn)
= d/dx[nxn-1] = n(n-1)xn-2 |
| Sum rule | d2/dx2[u(x) + v(x)] = d2/dx2 (u(x)) + d2/dx2v(x) |
| Difference rule | d2/dx2[u(x) – v(x)] = d2/dx2 (u(x)) – d2/dx2v(x) |
| Constant rule | d2/dx2(0) = 0 |
How to calculate the second-order derivative?
Following are a few examples to understand the second-order differential.
Example 1
Find the second derivative of 3x2 + 19x4 – 20y?
Solution
Step 1:First of all, calculate the first derivative of the given function. So, apply the differential notation to the given function.
d/dx (3x2 + 19x4 – 20y)
Step 2:Now apply the sum and the difference rules of differentiation.
d/dx (3x2 + 19x4 – 20y) = d/dx (3x2) + d/dx (19x4) – d/dx (20y)
Step 3:Apply the power and constant rules.
d/dx (3x2 + 19x4 – 20y) = 3d/dx (x2) + 19d/dx (x4) – d/dx (20y)
d/dx (3x2 + 19x4 – 20y) = 3 (2x2-1) + 19 (4x4-1) – 0
d/dx (3x2 + 19x4 – 20y) = 3 (2x) + 19 (4x3) – 0
d/dx (3x2 + 19x4 – 20y) = 6x + 76x3
Step 4:Now apply the differentiational notation again on the above equation.
d/dx [d/dx (3x2 + 19x4 – 20y)] = d/dx (6x + 76x3)
d2/dx2 (3x2 + 19x4 – 20y) = d/dx (6x + 76x3)
Step 5:Apply the sum rule.
d2/dx2 (3x2 + 19x4 – 20y) = d/dx (6x) + d/dx (76x3)
Step 6:Now apply the power rule.
d2/dx2 (3x2 + 19x4 – 20y) = d/dx (6x) + d/dx (76x3)
d2/dx2 (3x2 + 19x4 – 20y) = 6(1) + (76 * 3) x3-1
d2/dx2 (3x2 + 19x4 – 20y) = 6 + (228) x2
d2/dx2 (3x2 + 19x4 – 20y) = 228x2 + 6
Hence the second order differential of 3x2 + 19x4 – 20y is 228x2 + 6.
Example 2
Find the second derivative of x2cos(x) + 9x3 – 20sin(x) + x?
Solution
Step 1:First of all, calculate the first derivative of the given function. So, apply the differential notation to the given function.
d/dx (x2cos(x) + 9x3 – 20sin(x) + x)
Step 2:Now apply the sum and the difference rules of differentiation.
d/dx (x2cos(x) + 9x3 – 20sin(x) + x) = d/dx (x2cos(x)) + d/dx (9x3) – d/dx (20sin(x)) + d/dx (x)
Step 3:Apply the power, product, and constant rules.
d/dx (x2cos(x) + 9x3 – 20sin(x) + x) = d/dx (x2cos(x)) + 9d/dx (x3) – 20d/dx (sin(x)) + d/dx (x)
d/dx (x2cos(x) + 9x3 – 20sin(x) + x) = cos(x) d/dx (x2) + x2 d/dx (cos(x)) + 9d/dx (x3) – 20d/dx (sin(x)) + d/dx (x)
d/dx (x2cos(x) + 9x3 – 20sin(x) + x) = cos(x) (2x2-1) + x2 (-sin(x)) + 9(3x3-1) – 20(cos(x)) + (1)
d/dx (x2cos(x) + 9x3 – 20sin(x) + x) = cos(x) (2x) + x2 (-sin(x)) + 9(3x2) – 20(cos(x)) + (1)
d/dx (x2cos(x) + 9x3 – 20sin(x) + x) = 2xcos(x) – x2sin(x) + 27x2 – 20cos(x) + 1
Step 4:Now apply the differentiational notation again on the above equation.
d/dx [d/dx (x2cos(x) + 9x3 – 20sin(x) + x)] = d/dx [2xcos(x) – x2sin(x) + 27x2 – 20cos(x) + 1]
d2/dx2(x2cos(x) + 9x3 – 20sin(x) + x) = d/dx [2xcos(x) – x2sin(x) + 27x2 – 20cos(x) + 1]
Step 5:Apply the sum and difference rules.
d2/dx2 (x2cos(x) + 9x3 – 20sin(x) + x) = d/dx (2xcos(x)) – d/dx (x2sin(x)) + d/dx (27x2) – d/dx (20cos(x)) + d/dx (1)
Step 6:Now apply the product, power, and constant rules.
d2/dx2 (x2cos(x) + 9x3 – 20sin(x) + x) = d/dx (2xcos(x)) – d/dx (x2sin(x)) + 27d/dx (x2) – 20d/dx (cos(x)) + d/dx (1)
d2/dx2 (x2cos(x) + 9x3 – 20sin(x) + x) = cos(x) d/dx (2x) + 2x d/dx(cos(x)) – sin(x) d/dx (x2) – x2 d/dx (sin(x)) + 27d/dx (x2) – 20d/dx (cos(x)) + d/dx (1)
d2/dx2 (x2cos(x) + 9x3 – 20sin(x) + x) = cos(x) (2(1)) + 2x(-sin(x)) – sin(x) (2x) – x2 (cos(x)) + 27(2x) – 20(-sin(x)) + 0
d2/dx2 (x2cos(x) + 9x3 – 20sin(x) + x) = cos(x) (2) – 2x(sin(x)) – sin(x) (2x) – x2 (cos(x)) + 27(2x) + 20(sin(x)) + 0
d2/dx2 (x2cos(x) + 9x3 – 20sin(x) + x) = 2cos(x) – 2xsin(x) – 2xsin(x) – x2cos(x) + 54x + 20sin(x)
d2/dx2 (x2cos(x) + 9x3 – 20sin(x) + x) = 2cos(x) – 4xsin(x) – x2cos(x) + 54x + 20sin(x)
Hence the second order differential of “x2cos(x) + 9x3 – 20sin(x) + x” is “2cos(x) – 4xsin(x) – x2cos(x) + 54x + 20sin(x)”.
To avoid such a larger calculation of the second differential, you can use a second derivative calculator. You can get accurate results in a few seconds of the given function. Follow the steps below to calculate the second-order differential using this calculator.
Step 1: Write the function into the input box.
Step 2: Then select the variable.
Step 3: You can use the keypad icon to enter the mathematical symbols.
Step 4: Hit the calculate button below the input box.
Step 5: The result will show below the calculate button.
Summary
The process of finding the second-order differential is very simple. You have to apply the differential notation two times to calculate the second derivative. By following the above examples, you can solve any problem related to the second derivative.











